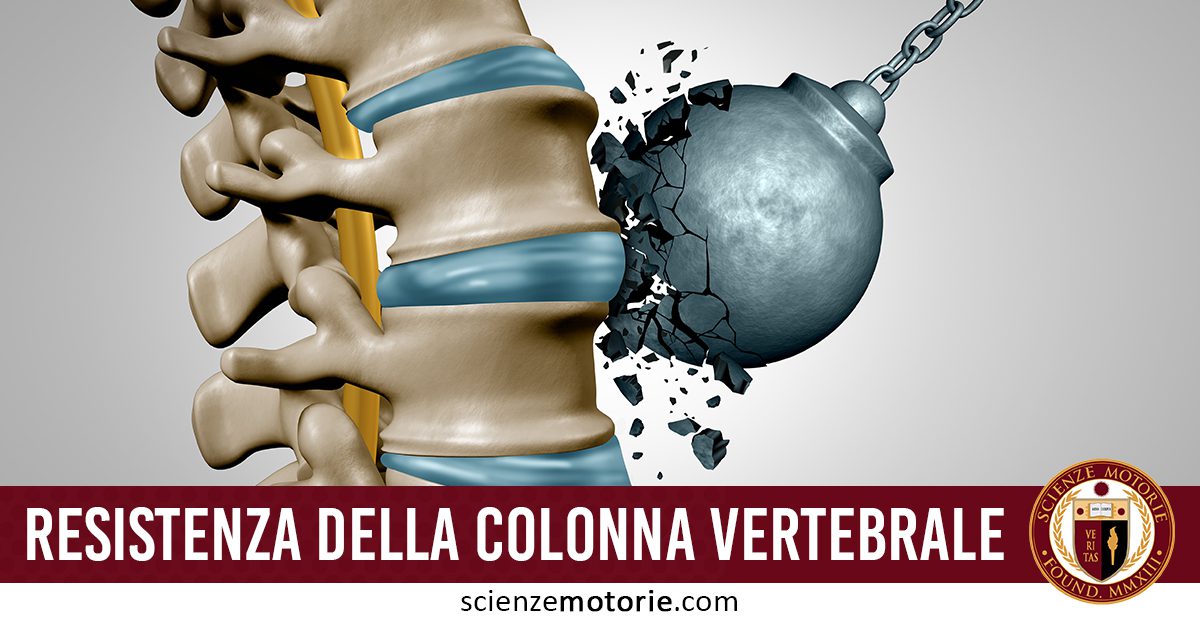
Una delle regole base che esiste nel mondo dello sport, e del movimento in generale, è che per evitare di sovraccaricare troppo la colonna vertebrale occorre conservare le curve fisiologiche il più possibile, durante l’esecuzione dei vari gesti.
Esiste una formula che molte persone hanno letto sui libri o studiato all’università che serve a calcolare la resistenza del rachide:
R= N2 + 1
Dove per N si intende il numero di curve mobili della colonna vertebrale. Questo significa che in presenza di 3 curve la resistenza sarà di 10 mentre, con una curva in meno, il risultato sarà dimezzato.
Su questo presupposto si basano correzioni tecniche, consigli pratici, analisi del movimento, ecc. di molti trainer, preparatori atletici e quant’altro. Il problema è che tutto questo è assolutamente sbagliato.
Dove nasce questa formula?
In ambito scientifico si dice sempre che ogni affermazione richiede delle prove in grado di confermarla, e che affermazioni sensazionali richiedono prove sensazionali. A questo punto si dovrebbero citare degli studi che dimostrino l’inefficacia di quella formula, tanto cara ed utilizzata da ogni esperto del movimento.
In realtà la questione è differente: è chi ha teorizzato quel calcolo che dovrebbe dimostrare quale attinenza esiste con la colonna vertebrale. Da dove è nata quella formula? Quali studi sono stati fatti per arrivare a quel punto? Il risultato che ne deriva rappresenta dei kg? Degli Newton? In base a cosa il numero delle curve va espresso al quadrato e perché bisogna aggiungere una unità? Con quella formula si calcola la resistenza a cosa? Al carico assiale, all’instabilità, alle rotazioni?
La grande popolarità di questa formula nasce dal fatto che è stata pubblicata all’interno del cosiddetto Kapandji: un testo che è stato di riferimento, per anni, nel campo del movimento. Se però si vanno a cercarne le fonti per capire come si è arrivati a quel calcolo non si troveranno studi, o indicazioni, di alcun tipo.
Fisica di base
Per venire a capo di questo enigma bisogna andare ad indagare nella fisica di base, e più precisamente nel carico critico euleriano per la teoria della trave elastica: una serie di formule che servono a calcolare come si deforma una trave quando soggetta ad un carico di punta, prima che questa si rompa.
Senza scendere eccessivamente nei dettagli, quello che è stato fatto da Kapandji, è semplificare il calcolo originale ipotizzando che la trave (nel nostro caso la colonna) avesse un vincolo di incastro alla base, tagliare la parte costante della formula e mantenere solo la variabile (che viene riportata come N) associandola al numero delle curve mobili.
In questo modo, dopo una serie di approssimazioni attuate senza alcun dato a supporto, è nata la formula che tutti conoscono.
La formula è comunque affidabile?
Senza andare a scomodare Eulero, si può affrontare la questione con una logica talmente semplice e banale da rendere incredibile il fatto che un calcolo simile sia stato studiato e divulgato, con tanta credibilità, fino ad oggi.
Esistono molti motivi per i quali non ha alcun senso usare quella formula. Ne elenchiamo alcuni.
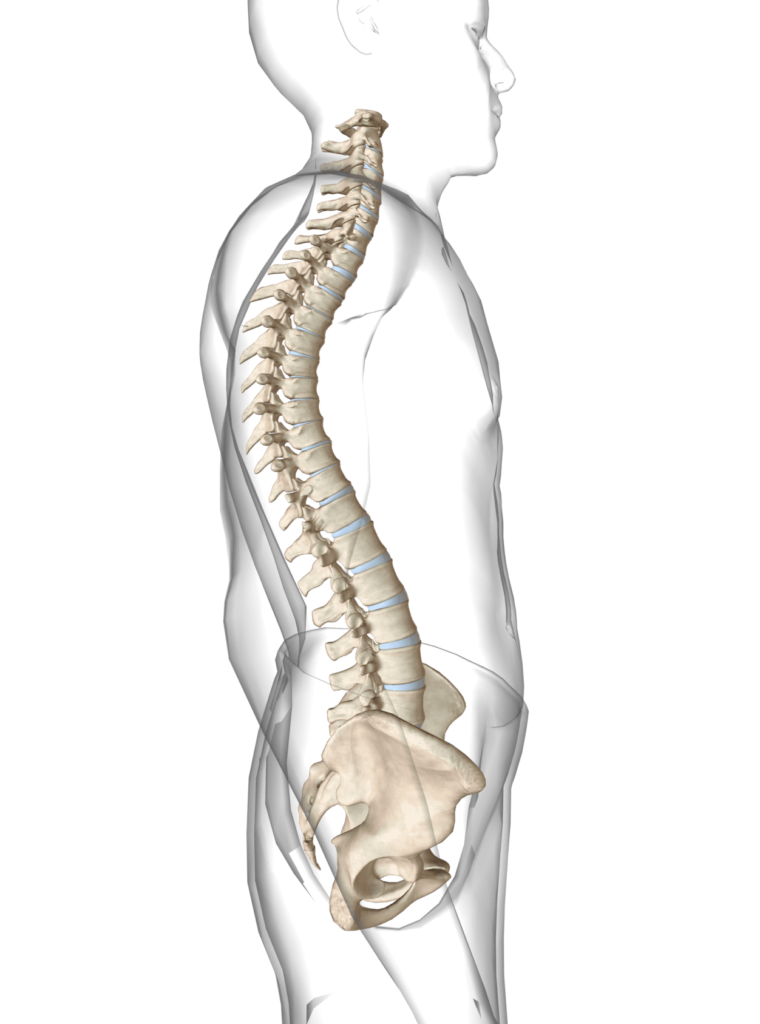
Tipologia delle curve
Nel calcolo, con la lettera N, si intendono indistintamente le 3 curve mobili del rachide: perdere una curva vorrebbe dire passare da una resistenza 10, ad una resistenza 5. Il problema è che questo vale per qualsiasi tipo di curva. Cioè: perdere la lordosi cervicale sarebbe equiparabile alla perdita della lordosi lombare. Perdere totalmente la cifosi dorsale porterebbe allo stesso identico risultato rispetto ad una rettilineizzazione del tratto cervicale.
Qualità delle curve
La formula indica semplicemente il numero di curve ma non vi è nessuna specifica riguardo ai requisiti che queste devono presentare. L’unica variabile da inserire nel calcolo è N. Ciò significa che avere delle curve eccessivamente sviluppate, poco sviluppate o nella norma, porta esattamente allo stesso risultato.
Vincoli
Nel calcolo la colonna vertebrale viene considerata come una struttura a sé stante ma questo è profondamente sbagliato. La presenza delle coste, del bacino, delle scapole, dei muscoli, dei legamenti, ecc. rappresentano un insieme di vincoli in grado di dissipare, veicolare e scaricare le varie forze in gioco. Non si può pensare di calcolare la resistenza della colonna senza considerare il contesto nella quale è inserita. Nel caso in cui si voglia fare un ragionamento del tutto teorico, pensando al rachide a sé stante, come se fosse una struttura separata dal resto del corpo, si incappa in due problemi:
- Questo calcolo sarebbe totalmente inapplicabile alla realtà, proprio perché la colonna vertebrale non si troverà mai in una situazione di totale isolamento.
- Se si eliminano tutte le strutture con le quali collabora, la colonna, non riesce a trovare una propria stabilità. Appare quindi molto relativo una formula utile a calcolare la resistenza di una struttura che non è in grado di rimanere in equilibrio in maniera autonoma.
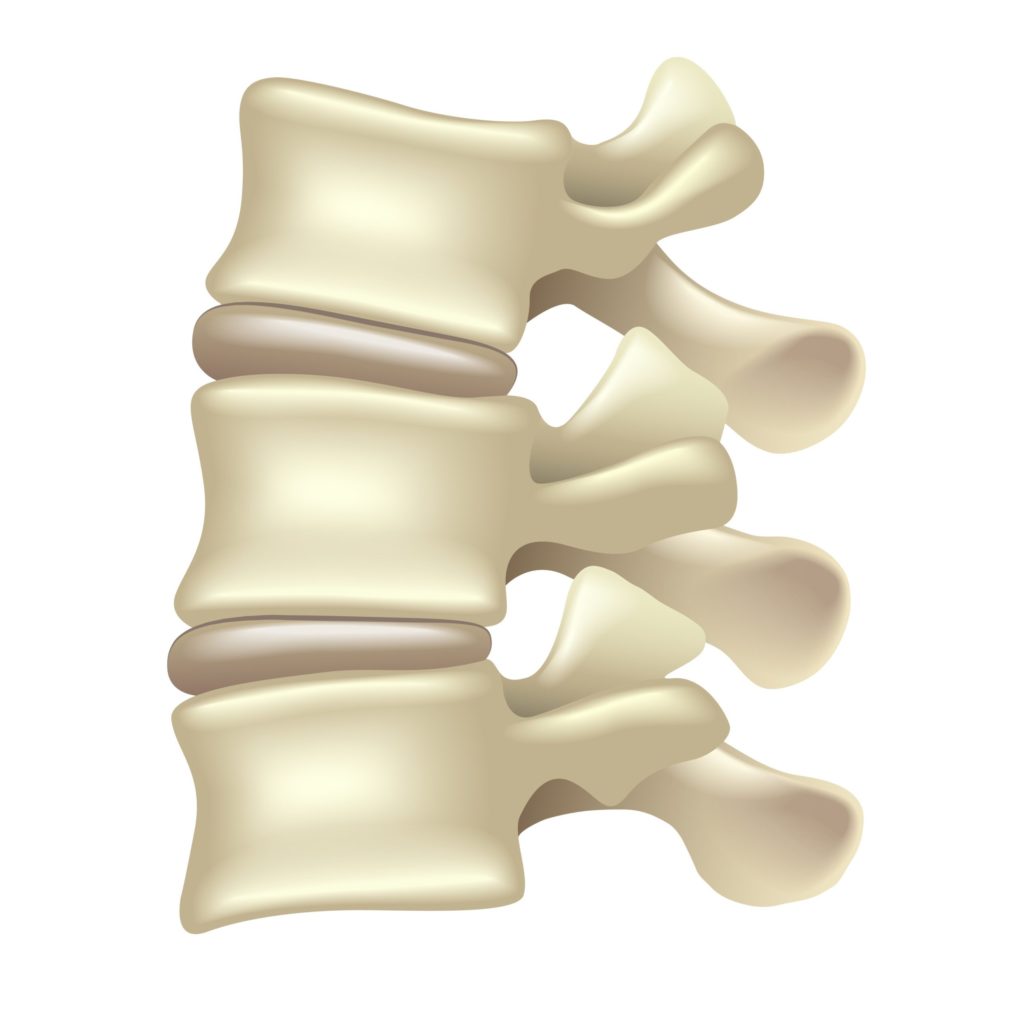
Dimensioni
Ogni singola vertebra del rachide ha una struttura differente rispetto alle altre. Questo significa che alcune saranno più voluminose, e con un diametro maggiore, rispetto ad altre: dovendo sorreggere l’intero peso del busto le vertebre lombari hanno una struttura decisamente diversa rispetto a quelle cervicali. Nella formula questo però non viene preso in considerazione, ipotizzando che tutte le vertebre del rachide abbiano lo stessi valore.
Contesto
Calcolare le curve della colonna vertebrale senza esaminare i muscoli con i quali questa interagisce, la qualità dei movimenti che è in grado di compiere, i possibili compensi presenti nella quotidianità, ecc. risulta quantomeno approssimativo. È infatti possibile trovare persone con tutte e 3 le curve intatte ma con grandi problematiche motorie, infiammazioni e dolori vari. Allo stesso modo è possibile notare soggetti con delle rettineilizzazioni del rachide che non presentano dolori né alcun tipo di disfunzione del movimento.
Importanza delle curve
A oggi, in letteratura, non esistono prove a sostegno che mantenere le curve fisiologiche preservi da dolori o problematiche varie. Non ci sono evidenze in grado di dimostrare che perdere la curva lombare, in vari movimenti, sia la sola ed unica causa scatenante del dolore, di lombalgie, di ernie, ecc.
Si potrebbe continuare a lungo nell’evidenziare le enormi falle, logiche e non solo, di quella formula. Il problema, infatti, non è dimostrarne l’inaffidabilità ma riuscire a trovare delle prove che la rendano efficace ed utilizzabile.
Purtroppo capita molto spesso di affidarsi a nozioni, teorie e concetti solo per il fatto che risultano popolari e generalmente accettati. Il primo passo per un professionista, specialmente di un ramo in continua evoluzione come quello delle scienze motorie, è quello di verificare ogni fonte ed ogni voce, per capire se ciò che sta facendo risulta ancora attuale ed efficace.